Il riferimento alla corda di una chitarra è uno degli esempi più semplici per spiegare il fenomeno delle onde stazionarie. Il video in aperture, manifesta il fenomeno fisico dell'onda stazionarie che si propaga fra due estremi vincolati. Il generarsi di tale onda è la conseguenza della sollecitazione indotta sulla corda, bloccata fra due estremi, come il caso di una chitarra o basso.
Onde stazionarie nodi e ventri
[ Figura 1 ]
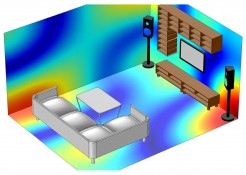
Come è facile notare dalla figura iniziale, la condizione affinchè nasca un'onda stazionaria, che solitamente si manifesta all'interno di uno spazio chiuso regolare, è la seguente: l'onda diretta incontrerà delle superfici, tipicamente pareti se consideriamo una stanza, le quali genereranno onde riflesse multiple che andranno a sovrapporsi tra loro dando luogo all'onda stazionaria.
Volendo capire a pieno il concetto, andiamo ad analizzare le relazioni matematiche che lo governano.
Consideriamo un'onda piana regressiva ed un'onda piana progressiva, rispettivamente:


Al contrario di ciò che si possa pensare, l'onda progressiva, nell'argomento del seno, presenta un segno - viceversa per l'onda regressiva che presenta un segno +.
Proviamo a spiegare il precedente, a prima vista, "tranello" matematico: In primis la funzione y(x,t) dipende da due variabili, x lo spostamento e t il tempo.
All'interno dell'argomento del seno abbiamo le due variabili indipendenti, appunto x e t, la lunghezza d'onda e la frequenza (che ricordo essere l'inverso del periodo). Dato per scontato l'andamento di una funzione sinusoidale, ed avendo chiarito che la precedente funzione y(x,t) rappresenta una perturbazione in movimento, analizziamo l'argomento del seno.
Consideriamo l'onda regressiva: in maniera molto semplice, immaginiamo l'onda che si propaga indietro, rispetto ad un riferimento spaziale, il tempo è una grandezza che può solo crescere detto ciò, se ad un dato istante temporale t1, ho una certa ampiezza dall'onda, tale valore d'ampiezza, ad un istante temporale t2 (t1 diverso t2) che sarà sicuramente maggiore di t1, lo ritroveremo in una posizione x, differente dalla precedente.
Questo poiché l'argomento del seno deve rimanere costante affinché l'ampiezza non vari, per tal motivo se t aumenta, x non può che diminuire affinché l'argomento rimanga costante e dunque l'ampiezza. Svelato l'arcano del segno + nell'onda regressiva. Tornando alla trattazione matematica, avremo che l'onda diretta e l'onda riflessa si vanno a sommare dando luogo a:

tramite la seguente relazione:

otterremo:

Dalla relazione ottenuta si evince che la posizione x ed il tempo t sono adesso separate. Ciò vuol dire che esisteranno posizioni x dove il seno sarà uguale a zero (nodi) e posizioni dove il seno sarà uguale a 1 (ventri). La cosa importante è che si hanno posizione fisse per i nodi e per i ventri senza avere propagazione, ma vi sarà una pulsazione continua in ampiezza in dipendenza della fase delle onde diretta e riflessa.
E' facile individuare le posizioni dei nodi e dei ventri (o antinodo come in fig. 1) considerando l'argomento del sin:

Ovvero il seno si annulla per multipli di pgreco, abbiamo trovato la condizione per i nodi.

Il seno è uguale a 1 per multipli di pgreco/2, abbiamo trovato la condizione per i ventri. Nelle precedenti, n appartiene ai naturali compreso lo 0. Vediamo in fig.1 che sono segnati i nodi a λ/2, proviamo a ragionare sulla condizione dei nodi:
Consideriamo n=0,1,2,3, 4…otterremo, rispettivamente, dalla prima condizione (quella sui nodi) x=0, λ/2, λ, (3/2)λ, 2λ…..
Mentre invece la condizione sui ventri, per n=0,1,2,3,4….otterremo rispettivamente: x= λ/4, (3/4)λ, (5/4)λ, (7/4)λ, (9/4)λ, …..
Abbiamo dunque, trovato le posizioni dei nodi e dei ventri. La distanza fra due ventri è di λ/2, mentre fra un un ventre ed un nodo di λ/4, come in figura1
ONDE STAZIONARIE IN AMBIENTE REGOLARE: LA NASCITA DEI MODI RISONANTI --->