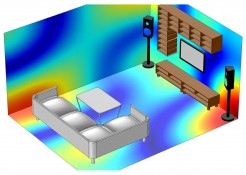
Le risonanze proprie o risonanze dell'ambientealtro non sono che onde stazionarie che si creano all'interno di ambienti regolari con pareti parallele. A tal proposito, considerando la distanza d fra due pareti parallele, la più bassa frequenza di onda stazionaria che può venirsi a creare è data dalla seguente relazione:

Inoltre considerando quest'altra formula:

andremo ad ottenere le onde stazionarie di ordine superiore o modi di ordine superiore. In entrambe le formule v=344m/s (velocità del suono in aria).
Facciamo due conti: ipotizzando due pareti parallele ad una distanza d=6m, il mezzo in cui si propaga l'onda è l'aria, calcolando i primi 5 modi otterremo:
n=1 f=28,66Hz
n=2 f=57,33Hz
n=3 f=86Hz
n=4 f=114,66Hz
n=5 f=143,33Hz
Modi assiali, tangenziali e obliqui in ambiente regolare
[ Figura 2 ]
Purtroppo non è mai così semplice. Abbiamo detto che una coppia di pareti parallele genera onde stazionarie (modi assiali) e in tutti gli ambienti, quasi sempre a forma di parallelepipedo, abbiamo almeno tre coppie di pareti parallele. Inoltre dobbiamo anche considerare i modi tangenziali e modi obliqui, ovvero quelli prodotti da riflessioni anche tra pareti adiacenti e non parallele (Figura 2). E’ facile intuire che l’intensità delle onde riflesse si andrà ad attenuare man mano che aumentano le riflessioni. Se ne deduce che i modi assiali sono i più dannosi perché nei modi obliqui il segnale sonoro deve essere riflesso molte volte prima di poter giungere alle nostre orecchie.
"Qui di sotto un piccolo approfondimento sui modi assiali, tangenziali e obliqui con un comodo calcolatore. Sono presenti i profili modali (di ordine differente) al fine di acquisire consapevolezza sul loro comportamento.
P.s. cliccate sul pulsante per accedere alla pagina!"
Velocità di propagazione del suono in differenti materali
La velocità di propagazione del suono (v) varia da materiale a materiale. Ecco qualche esempio (Tabella 1):

Velocità di propagazione del suono in differenti materiali
[ Tabella 1 ]
Alla frequenza in cui si instaura un'onda stazionaria, o ai suoi multipli, si crea un incremento del livello acustico, con conseguenti code sonore visibili nella waterfall con e senza risonanze (Figura 3).

Waterfall con risonanze e senza risonanze
[ Figura 3 ]
L'effetto è massimo se l'eccitazione avviene nel ventre dell'onda (cioè alle estremità dove vi è il massimo di pressione). Se, invece, l'eccitazione avviene a metà parete (o a metà dell'elemento in cui avviene il fenomeno) si ha che il corrispondente modo assiale risulta scarsamente eccitato. Ovviamente, poiché vi sono sempre più onde stazionare gli effetti si misceleranno e si distribuiranno. Quando una dimensione è però prevalente, l'onda stazionaria corrispondente diventa molto più avvertibile e dannosa.
Proviamo a fare degli esempi elementari dove il mezzo di propagazione del suono è l’aria è le onde stazionarie che si creano sono all'interno di un ambiente regolare (Tabella 2):

Calcolo onde stazionarie in ambiente regolare in aria
[ Tabella 2 ]
<---- ONDE STAZIONARIE: FRA UN NODO ED UN VENTRE SI SCOPRE IL PIZZICATO DI UNA CHITARRA
LE ONDE STAZIONARIE ALL'INTERNO DEI PANNELLI: CALCOLO RISONANZE ---->